sysarmy-sueldos-2020.1

Predicción de sueldo

Por Sebastián Waisbrot

Vamos a ver cómo crear un modelo de machine learning que pueda determinar el sueldo de una persona según información personal y laboral. El código está disponible en github, en este texto vamos a exponer el razonamiento y explicar las técnicas utilizadas.

Qué es un modelo

Un modelo busca representar matemáticamente relaciones entre entidades para estudiar su comportamiento. En este caso en particular, vamos a ver cómo a partir de cierta información específica de una persona (género, edad, años de experiencia, etc.) y de su trabajo (cantidad de empleados, rubro, etc.) podemos inferir, con cierto grado de precisión, su sueldo.

Qué es un modelo de machine learning

El objetivo de machine learning (o aprendizaje automático) es desarrollar técnicas para que las computadoras aprendan. Esto implica darle un conjunto de datos a la máquina para que generalice cierto comportamiento que, después, pueda aplicar a datos nunca “vistos” y así logre realizar predicciones e inferencias. En general una persona puede hacer modelos con los parámetros que quiera, pero dentro de esta área en particular, sus valores son determinados automáticamente.

Metodología

A continuación desarrollaremos, paso a paso, dos modelos. Vamos a hacer un breve análisis de los datos y, también, vamos determinar cómo evaluaremos a esos modelos, ya que queremos saber cuán bueno es reflejando la realidad. Luego, para cada modelo, vamos a determinar qué arquitectura va a usar. Esto quiere decir, por ejemplo, que si va a seguir una fórmula matemática, deberemos decidir qué forma va a tener. Después hay que procesar los datos de alguna manera para que el modelo pueda usarlos; esto va a depender de la arquitectura. Y por último, vamos a evaluarlos los modelos.

Origen de datos

La información que vamos a usar como base es la encuesta de sueldos de sysarmy 2020.1. Esta encuesta se realiza cada seis meses anónimamente y luego los microdatos (cada respuesta recibida) son publicados. Las respuestas corresponden al período 9/12/2019 - 3/2/2020, para un total de 5.982 personas.

Para obtener esta información, sysarmy crea un formulario y publica el link en redes sociales y grupos de usuarios de tecnologías relacionadas. Por ello hay que considerar que las respuestas son de una población autoseleccionada, y por lo tanto no representan a toda la población de IT de Argentina. Cada vez que lleguemos a una conclusión tenemos que tener en cuenta que no se puede generalizar sino que, como mucho, se puede apreciar una tendencia.

También tenemos que tener cuidado con la calidad de la información. Como el formulario es abierto para que cualquier persona ingrese los datos que quiera, no se puede estar seguro de la calidad de los mismos. Por ejemplo en esta edición alguien respondió que tiene 1.555.555.555.555.555.555.555.555 empleados a cargo, un número claramente exagerado. Sin embargo puede haber otros casos donde no se detecten tan fácilmente los problemas, o incluso que la información sea verosímil y no sea posible de diferenciar.

Los datos corresponden a los meses de diciembre de 2019 y de enero de 2020 en Argentina, meses en los cuales la inflación fue de 3,7% y 2,3% respectivamente. Esto puede traer variabilidad en los números porque no tenemos la fecha de cada registro para normalizar los valores si hubo ajustes de sueldo.

Detección de anomalías

El primer paso, considerando el origen de los datos, va a ser “limpiar” la información. Queremos eliminar valores extremos que nunca serían posibles, números que un humano encuestando no hubiese aceptado. Para eso podemos graficar cada columna y buscar números que no tengan sentido.

Un par de ejemplos:

En el gráfico (a) vemos que alguien respondió que ganaba alrededor de $7.000.000.000.000 de pesos por mes. Si eliminamos ese dato, que claramente no es válido, obtenemos el gráfico (b). Pero, además, vemos que muchas otras personas pusieron que ganaban $1, quizás personas desempleadas que igual querían participar de la encuesta (gráfico (c)). Si también eliminamos esos valores, entonces obtenemos el gráfico (d).

Por otra parte, en el gráfico (e) una persona puso que tenía alrededor de 2000 años en la misma empresa, probablemente alguien que malinterpretó la pregunta como desde qué año estaba en la empresa actual. Si eliminamos ese dato, obtenemos el gráfico (f).

Una vez hecha esta “limpieza”, tenemos los datos con los cuales vamos a trabajar para construir nuestro modelo.

Criterio de evaluación

Los modelos tienen dos etapas, una de entrenamiento y una de predicción. En la etapa de entrenamiento, reciben datos con sus etiquetas que representan el resultado correcto, en este caso, el sueldo. En la de predicción, el resultado correcto es desconocido y tienen que declarar su opinión. Sería muy sencillo hacer un modelo que memorice las respuestas correctas y las responda siempre que se les pregunte por una de ellas, pero, pese a poder predecir perfectamente estos valores, este modelo tendría poca capacidad de predicción frente a datos desconocidos que no se ajusten exactamente a aquellos de los que aprendió.

Entonces, lo que necesitamos es entrenar con un conjunto de datos conocidos y evaluar otro conjunto de datos, también conocidos, pero que el modelo no haya “visto” nunca. De esta manera podremos saber cuán bueno es el modelo. Como los datos que tenemos son relativamente pocos, vamos a utilizar una técnica denominada validación cruzada (o cross validation), que consiste en dividir los datos en varios grupos y entrenar el modelo varias veces. En cada una de esas veces, vamos a excluir un grupo diferente del entrenamiento y lo vamos a usar para la predicción. De esta forma, si hacemos validación cruzada con cinco grupos vamos a entrenar cinco modelos diferentes, cada uno con cuatro quintas partes de los datos, y vamos a pedirle que infiera los datos del grupo restante.

Así, una vez terminado el proceso, tendremos una predicción para cada valor, alcanzada por el modelo que no “vio” ese dato al entrenarse. Una vez disponibles las predicciones queremos saber cuán cercanas al resultado correcto eran. Para eso podemos calcular un coeficiente de determinación (o r2) que nos va a decir la proporción del error. Por ejemplo si una persona gana $100 y el modelo estima $110 y para otra que gana $200 predice $180, su coeficiente es de 0.9, porque tiene un 10% de error en cada estimación. El mejor coeficiente posible es 1, equivalente a decir que todas las predicciones fueron aciertos.

Modelo base

Elegir arquitectura

Basado en trabajo previo, sabemos que hay tres características que son buenas predictoras del sueldo de una persona: el género, la provincia en que trabaja y cuántos años de experiencia tiene. Entonces, un modelo sencillo que podemos construir consiste en tomar en cuenta sólo estas características y tratar de ubicar la línea recta que más cerca pase de los puntos, o sea, armar un modelo de regresión lineal como el que se muestra en el gráfico (g).

Preparar los datos

Para usar este modelo tenemos que llevar cada característica a un espacio lineal. Que el espacio sea lineal significa que se puede medir la distancia entre dos puntos y que esa misma distancia tendrá el mismo valor en otro lugar de la escala.

Tenemos datos de dos tipos: numéricos (la experiencia y el sueldo), es decir que podríamos directamente operar con ellos, y no numéricos (el género y la provincia), a los que vamos a tener que transformar en números de alguna manera.

Datos numéricos

En cuanto a la experiencia, si bien ya tenemos números con los que podemos hacer cuentas, podríamos pensar que no es lo mismo para el sueldo pasar de no tener experiencia a tener 1 año, que de tener 10 a 11. La diferencia parece ser decreciente, es decir que mientras más años de experiencia tenga una persona, menos le va a significar, en el sueldo, la adición de uno nuevo.

.

Una buena manera de ajustar este comportamiento es usando una función logarítmica porque nos permite transformar un número en otro manteniendo el orden pero achicando la distancia con el siguiente a medida de que el número se hace mayor. En el gráfico (h) vemos como el valor correspondiente a 1 está más lejos del de 0 que el correspondiente al 7 respecto del de 6.

También podrímos aplicar logaritmo al salario porque no es lo mismo ganar $1.000 más para alguien que gana $10.000 que una persona que cobra $200.000.

Datos categóricos en modelo lineal

¿Cómo podemos ponerle números a datos categóricos que reflejen linealmente las diferencias en cada caso? Una opción sería asignarle a cada “provincia” el “sueldo promedio de la provincia”. Tenemos que tener en cuenta que cuando recibamos datos para estimar, no vamos a saber el sueldo de esa persona, entonces, en principio, podríamos asignarle el promedio que calculamos de la provincia en la que vive como un indicador de su salario. De esta manera, si el salario promedio de la Provincia de Buenos Aires y el de Santa Fe son parecidos, la provincia va a aportarle un valor similar y cercano a dos personas que vivan en esos lugares, mientras que si Jujuy tiene un promedio más bajo, la diferencia respecto de las personas que viven en Santa Fe y Buenos Aires será mayor.

Lo mismo se puede aplicar para género usando como valor el promedio de sueldo para hombres, mujeres y otros.

Evaluación

Con estas transformaciones, podemos aplicar validación cruzada para entrenar cinco modelos de regresión lineal y calcular el r2 promedio resultante. Al hacerlo, obtenemos un valor de 0.2398. Es decir que este modelo sencillo ya puede explicar casi el 24% del sueldo de las personas.

Elección de modelo final

Elegir arquitectura

La encuesta provee mucha información para cada persona y cada respuesta puede tener efectos distintos al interactuar con otra. Por ejemplo, manejar el lenguaje Python no significa necesariamente lo mismo para un desarrollador que para un científico de datos, porque los usan de forma diferente.

Un tipo de modelo basados en árboles de decisión aprovecha este tipo de relaciones. Vamos a usar uno llamado xgboost porque suele ofrecer buenos resultados.

Preparar los datos

Datos geográficos

La encuesta recolecta información geográfica a nivel provincia. El costo de vida en cada provincia es bastante desparejo y los sueldos también suelen serlo. Por eso, como dijimos antes, sirve como predictor. Pero hay provincias que tienen muy pocas respuestas y eso dificulta la generalización. Recordemos que los datos en pequeña escala no son confiables por la forma de la encuesta así que tratemos de agruparlos en bloques más grandes.

Cantidad de respuestas por provincia.

Provincia	Cantidad de respuestas
Ciudad Autónoma de Buenos Aires	3961
Catamarca	2
Chaco	33
Chubut	21
Corrientes	16
Entre Ríos	39
Formosa	3
Jujuy	13
La Pampa	2
La Rioja	7
Mendoza	109
Misiones	21
Neuquén	25
Río Negro	21
Salta	10
San Juan	6
San Luis	6
Santa Cruz	2
Santa Fe	279
Santiago del Estero	4
Tucumán	26
Córdoba	310
Provincia de Buenos Aires	431
Tierra del Fuego	5

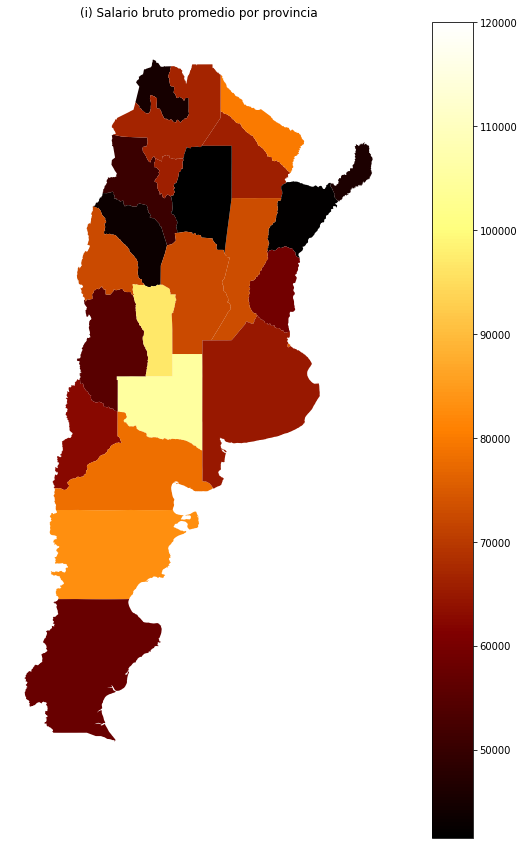
El problema es que hay muy pocos datos fuera de la Ciudad de Buenos Aires, la Provincia de Buenos Aires, Santa Fe y Córdoba. Lo que podríamos hacer es analizar los sueldos promedio en cada provincia (gráfico (i)). Esto nos puede dar una idea de qué provincias, que tengan pocos datos, podrían formar parte de un mismo bloque porque consideramos que tienen similitudes culturales y esperamos que el comportamiento sea semejante.

Ver detalles

A partir de este análisis, podríamos pensar en dividir a las provincias de la siguiente forma:

• Noroeste: Catamarca, Jujuy, La Rioja, Salta, Santiago del Estero, Tucumán.
• Noreste: Chaco, Corrientes, Entre Ríos, Formosa, Misiones.
• Cuyo: Mendoza, San Juan, San Luis.
• Llanura Pampeana: La Pampa, Santa Fe, Córdoba, Provincia de Buenos Aires.
• Patagonia: Chubut, Neuquén, Río Negro, Santa Cruz, Tierra del Fuego.
• AMBA: Ciudad de Buenos Aires y Gran Buenos Aires.

La decisión de cómo agrupar las provincias es en parte arbitraria y podría hacerse distinto. Por ejemplo, San Luis y La Pampa, con pocos registros, no se parecen tanto a ninguna provincia de la zona.

Ahora que tenemos las regiones, podríamos usar el promedio de cada región en lugar del promedio de cada provincia en nuestro modelo. Sin embargo, podemos también pensar en otras alternativas que nos darían mejores resultados para características categóricas (región, género, etc.).

Datos categóricos

Si bien el modelo de regresión lineal es sencillo, nos da opciones limitadas. Podemos expandir nuestras posibilidades usando otro modelo en el que asignemos valores binarios a las características categóricas.

Por ejemplo, para el caso de las regiones, podemos usar una columna por cada región y asignarle a cada persona un valor binario para cada columna. Entonces alguien de AMBA va a tener un verdadero en esa columna (1) y un falso en Patagonia (0), Llanura Pampeana (0), etc. De esta manera iremos construyendo una matriz.

Lo mismo podemos hacer para características que no son mutuamente excluyentes, como los lenguajes de programación que sabe una persona. La ventaja de este enfoque es que pueden seleccionarse múltiples opciones y esa información puede verse reflejada en la matriz.

Las características que tengan pocas ocurrencias pueden ser eliminadas dado que no proveen información para que el modelo pueda aprender.

Entonces, una persona de la Ciudad de Buenos Aires, hombre, que usa Java y JavaScript en su trabajo será representado de la siguiente manera:

Columna	Valor
Me identifico=Hombre	1
Me identifico=Mujer	0
region=AMBA	1
region=Pampa	0
region=Patagonia	0
…	…
Lenguajes de programación=javascript	1
Lenguajes de programación=java	1
Lenguajes de programación=rust	0

Evaluación

Usando XGBoost, un modelo basado en árboles de decisión que suele tener buenos resultados, y con las técnicas mencionadas anteriormente, obtenemos un r2 promedio de 0.5175. Es decir que ya podemos explicar más de la mitad del sueldo con nuestro modelo. Todavía se puede mejorar, por supuesto.

A futuro

Queda pendiente analizar cuán justo es el modelo y si se puede hacer una variante mejor en ese aspecto. Por ejemplo, una de las características que incorporamos fue género y el modelo podría usar esta información para perjudicar a un grupo. Sacarla no necesariamente es suficiente para solucionar este problema.

El modelo puede mejorarse de incontables formas. Para enumerar algunas de ellas:

• Describir mejor las tecnologías. Hoy en día cada lenguaje, framework, stack está sólo descripto por su nombre. Sin embargo, en la práctica, algunas se parecen entre ellas más que otras. Por ejemplo Microsoft Azure es más parecido a Amazon Web Services que a Solaris. Este tipo de relaciones que conocemos puede reflejarse en los datos pero, como la muestra es relativamente pequeña, puede no ser suficiente, así que usar una fuente externa que informe al modelo sobre las tecnologías podría mejorar los resultados.

• Selección de características. Casi toda la información brindada fue dada al modelo para que establezca las relaciones. Con un poco de trabajo se pueden quitar las menos relevantes y esto podría ayudar a encontrar mejores inferencias.

• Búsqueda más profunda de anomalías. Se podría usar el modelo actual para encontrar casos sospechosos de ser anómalos y candidatos a exclusión.

This site is open source. Improve this page.